Semántica

Richard Feynman, los alfabetos y los lenguajes

Barron Romero Carlos *
Mager Hois Jesús Manuel **
Reyes Avilés Fernando ***
UAM-A

Resumen El análisis de los lenguajes se ha convertido en una tarea multidisciplinaria que se ha involucrado desde la lingüística misma hasta la teoría de la computación. El proceso de comunicación también es un problema de computación, es en este contexto que Richard Feynman se adentra a la discusión sobre la equivalencia de lenguajes en el marco de la universalidad de los mismos, únicamente diferenciada por la extensión de sus libros. En el trabajo se concuerda con Feyman sobre la inexistencia de un mejor lenguaje, pero que que cada uno de ellos encierra conocimientos únicos adquiridos a través de un proceso histórico particular. Esto se puede comprobar con el proceso de traducción en el cual no es posible transferir íntegramente toda la información contenida en el lenguaje fuente al destino. Es por ello que la extinción de una lengua es una pérdida para la semántica universal. Feynman también plantea el mismo problema sobre los alfabetos, donde tampoco existe un óptimo. Sin embargo, en este punto es posible comprobar que el alfabeto óptimo es uno terciario. Esto plantea un punto a discusiones futuras especialmente para las computadoras que hoy en día funcionan con un alfabeto binario.

Summary The analysis of languages ​​has become a multidisciplinary task that has been involved from linguistics itself to the theory of computation. The communication process is also a computer problem is in this context that Richard Feynman enters the discussion on the equivalence of languages ​​within the framework of the universality of the same, differentiated only by the extent of his books. In the work is consistent with Feyman about the lack of a better language, but each of them holds unique knowledge acquired through a particular historical process. This can be checked with the process of translation which is not possible to fully transfer all the information contained in the source language to the target. That is why the extinction of a language is a loss for the universal semantics. Feynman also poses the same problem on the alphabets, where there is not optimal. However, at this point it is possible to verify that the optimal alphabet is one tertiary. This raises a point for future discussions especially for computers today operate with a binary alphabet.

Palabras clave Lenguajes, Traducción, Alfabeto óptimo, Semántica.

Keywords Languages, Translation, Optimal Alphabet, Semantics.

---

 

Introducción

Richard P. Feynman, al analizar la universalidad del lenguaje plantea las siguientes preguntas: ¿Cuál es el mejor lenguaje para describir algo?  ¿Cuál es el mejor alfabeto, por ejemplo, para el idioma inglés? . Él comienza analizando la universalidad de los lenguajes basándose en la eficiencia que tienen para transmitir información. Posteriormente, profundiza más en el tema al incluir en la discusión la efectividad de un alfabeto de 26 símbolos.

Dado que los lenguajes son una importante herramienta de comunicación, las preguntas planteadas por Feynman tienen repercusiones tanto en computación, cómo en las relaciones humanas. Hoy en día, debido al proceso de globalización que están sufriendo los lenguajes, es vital reflexionar sobre el tema. Feynman afirma que no existe un mejor lenguaje o un mejor alfabeto. Pero, ¿si no existiera diferencia entre los lenguajes, qué sentido tendría la existencia de tanta variedad?  A continuación se analizarán sus ideas acerca de este tema. Primero se discutirá la afirmación de que no existe un mejor alfabeto y después se revisara la existencia de un mejor lenguaje.

El mejor alfabeto

Feynman afirma que las 26 letras del inglés no son relevantes para expresar el lenguaje, ya que se podría usar cualquier conjunto de símbolos, cómo lo son los tres del código morse, o dos del código binario; por lo que se podría elegir el conjunto de símbolos con bastante libertad.

Sin embargo, esto no es correcto. La cardinalidad del conjunto de símbolos de un alfabeto sí influye directamente en la capacidad para expresar información del mismo. Para el valor 99 en un sistema decimal se requeriría de veinte símbolos (10 por cada orden), mientras que si usáramos un sistema binario esos mismos símbolos podrían agruparse en diez pares (2¹⁰). Pero, la misma cantidad de símbolos en un alfabeto decimal únicamente podría expresar 100 valores, mientras que con un alfabeto de dos símbolos 1024. S.V. Fomin (Fomin, 1975:35) generaliza esta característica como:

donde n es el número de dígitos y x es la base del sistema. Esta expresión es una función de x para todo x∈R,x≥0. La función descrita por la ecuación (1) tiene un máximo, el cual indica el número óptimo de símbolos en el alfabeto de un lenguaje para obtener la mayor cantidad de valores o estados posibles. El valor máximo de la función se obtiene al derivarla e igualarla a cero cómo se muestra en (2).

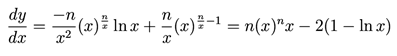
Al realizar esta igualación se obtiene el número e, que aproximadamente es 2.71828. Si regresamos a los sistemas de numeración, e se encuentra más cerca de 3 que de 2. Con lo cual podemos plantear que un alfabeto de tres símbolos es el mejor, ya que logra optimizar la información que representa.

El mejor lenguaje

El problema de la determinación de un lenguaje mejor es complejo, ya que establecer un criterio o cualidad para definir si un lenguaje es mas universal o más eficiente que otro tiene muchos aspectos difíciles de conciliar. Feynman clasificó, en forma práctica, la eficiencia de los lenguajes en términos de tamaño de los libros, “ninguno de estos elementos es inherentemente mejor que cualquiera de los otros: todos hacen su trabajo, y se diferenciarán únicamente en eficiencia”(Feynman, 1997:2). Sin embargo, cada lenguaje existe en un contexto histórico y social propio y contiene información, no únicamente en la esfera sintáctica, sino también en la semántica por lo cual no podría existir una equivalencia estricta.

Los lenguajes modelan eventos de un entorno natural o social, así como las ideas del pensamiento humano, y cada uno de ellos lo realiza de manera diferenciada aprovechando sus reglas gramaticales y su acervo de palabras o sílabas válidas. Existen diferencias entre los lenguajes humanos, los cuales poseen características propias. Un artículo científico, debido a que está escrito de manera formal, puede ser traducido sin mucha complicación, sin embargo, la propiedad que poseen los lenguajes de contener emociones, ideas y conceptos, que no pueden ser expresados únicamente por medio de las palabras, es lo que vuelve tan difícil la traducción de poemas, canciones, etc.

Sintácticamente no existe problema alguno, ya que a falta de alguna definición, simplemente se inventa o se importa de algún otro lenguaje. Frente a la falta de palabras suficientes para la explicación de un cierto concepto en un idioma, Feynman nos comenta que bastaría con incorporar esa palabra al vocabulario ya existente, o crear una nueva. Un claro ejemplo de esta idea es la palabra “tuitear”, la cual no existía en el español hasta hace unos años, pero debido a que surgió la necesidad de describir la acción de escribir un mensaje en la red social Twitter mediante una palabra, se decidió agregarla al acervo de palabras ya existentes.

Alfred Tarski, concluyó que un lenguaje natural no formalizado es más expresivo que uno restringido, lo que permite que uno solo de sus elementos tenga múltiples significados. Al momento de tomar el concepto de verdad, se podría derivar del mismo su propia negación. Esta idea está formulada en el Teorema de Indefinibilidad de la Verdad de Tarski (Traski, 1936: 18), y nos permite entender el motivo por el cual no es posible traducir sin pérdida de información, y no sería posible definir la existencia de un mejor lenguaje. La idea básica del teorema de Tarski es que el concepto de “fórmula verdadera” en un lenguaje formal de orden finito tiene una definición correcta con expresiones lógicas de la misma lengua y con términos de su propia morfología, pero bajo la condición de que el metalenguaje con el cual se construye sea de un orden superior que la lengua que describe. Para un lenguaje formal de orden infinito será necesario insertar el concepto de verdad en el metalenguaje y definir sus propiedades fundamentales con ayuda del método axiomático. Sin embargo, esto no es posible en un lenguaje natural, en contraste con la lengua formal, debido a su universalidad, que lleva al ámbito semántico cada palabra o expresión. Este aspecto semántico es tan variable que incluso entre dos individuos que hablan el mismo lenguaje, al momento de utilizar cierto concepto, no se puede garantizar que la comprensión sea la misma. Para ilustrar esta idea se presentan dos ejemplos.

Primero se revisará una parte del poema Das Lied vom Klassenfeind poema de Bertold Brecht (Brecht, 1997: 214). Fue creado en la época de auge fascista en Alemania y describe la postura de la resistencia.

Da mag dein Anstreicher streichen Den Riß streicht er uns nicht zu! Einer bleibt und einer muß weichen Entweder ich oder du.

¡Puede tu pintor pintar La grieta no nos la puede tapar!  Uno perdura y el otro tiene que orillarse o tú o yo.

La traducción al español no puede ser fiel al original por la palabra Anstreicher, que en traducción literal sería pintor y que concuerda con todo el resto de la estrofa a la perfección. Sin embargo, en alemán esta palabra también significa: aquel que organiza maliciosamente algo. Si bien podría ser descrito en un nuevo verso, perdería la concordancia con el resto del texto, con lo cual se vuelve imposible encontrar en todos los lenguajes naturales un equivalente a las palabras de otro. Se juega con el agitador fascista y el pintor que intenta cubrir las diferencias en la sociedad alemana, donde la misma palabra expresa dos significados que explican el mismo fenómeno. Algo imposible de expresar fuera del contexto del idioma particular. Los problemas de traducción entre dos lenguajes son una cuestión común, debido a que no existe un equivalente en forma de un mapeo directo entre ellos. Recordemos que modelar no excluye la posibilidad de que un lenguaje pueda expresar de manera diferenciada los fenómenos, lo cual traería una evaluación cualitativa y cuantitativa de la descripción. Los lenguajes más semejantes, pero sobre todo los que han compartido más aspectos históricos, siempre tendrán la mayor facilidad de modelarse unos a otros. El problema surge cuando son muy diferentes.

En el segundo ejemplo se presenta el wixárika (también conocido como huichol), idioma perteneciente a la familia utoazteca, que funciona como un idioma aglutinante entorno al verbo, completamente diferente al alemán y al español. Al verbo se le puede incorporar 18 prefijos y 23 subfijos (Iturrio, 1999: 211), con lo que existe la posibilidad muy amplia de construcción de palabras. En el ejemplo siguiente se muestra como se construye el concepto de montaña.

hai m-a-ta-ka-i-t+ka

Donde hai significa nube, y la palabra siguiente es el verbo matakait+ka, que se divide en sílabas como se muestra arriba. La combinación entre m y a refiere a algo figurativo, el ta a algo que está al borde de, ka localiza esto en cierto espacio, la i significa estar, mientras que t+ka es plural. Con lo que podemos leerlo cómo “donde las nubes bordean", y que en una manera muy generalizada se traduciría como montañas (Gomez, 1999:54). En español es difícil acercarse a la comprensión de este concepto, lo cuál se puede lograr explicándolo. Únicamente con un contexto y conocimiento a fondo de aquellos lenguajes entre los cuales se desea encontrar una equivalencia, no sólo a nivel gramatical, sino también a nivel cultural será posible crear una traducción aceptable, pero no completa, ya que un idioma es el reflejo de la cultura de aquellos que lo utilizan.

Si tomamos la parte sintáctica, idiomas como el inglés con poca variabilidad en sus palabras clasificados como analíticos, o idiomas fusionantes como el alemán o español son muy diferentes a los idiomas polisintéticos como la mayoría de las lenguas originarias del continente americano. Bajo la forma de construcción de un verbo en wixárika es posible obtener 312 063 515 688 960 000 000 verbos1 a partir de una única raíz verbal, lo cual vuelve a este lenguaje muy versátil, sin contar con modificaciones a los sustantivos. Si comparamos esto con las 171,476 palabras del Oxford English Dictionary encontramos una gran diferencia. El estudio, A cross-linguistic perspective on speech information rate, revela que aquellos lenguajes con una tasa silábica alta tienen una densidad de información menor a la hora de una comunicación humana hablada. La eficiencia no está directamente relacionada con el tamaño de nuestros libros pero el aprendizaje de un idioma si cambia dependiendo del número de tiempos verbales y la cantidad de palabras que hay en él.

Conclusiones

Cada lenguaje natural surge en un proceso cultural e histórico, adoptando una estructura para poder modelar la realidad y las ideas humanas, conservando sus matices y peculiaridades. Por ello no se puede explicar únicamente desde sus aspectos puramente gramaticales o sintácticos donde sería posible tener una traducción entre ellos; sino que se extienden al terreno semántico que es indefinible, ya que una palabra puede adquirir muchos significados diferentes. Esta riqueza encerrada en sus palabras y expresiones se pierde, en cierto grado, a la hora de traducirse a otro lenguaje como se ha ejemplificado en el texto. La eficiencia a la cual se refiere Feynman, tomando la extensión de los libros, es irrelevante respecto a la expresividad de la gran variedad de lenguajes humanos.

Dado que no existe una traducción sin pérdida de información, cada vez que un lenguaje desaparece, la humanidad pierde una parte de su semántica universal. Impulsar un lenguaje por su eficiencia o facilidad de aprendizaje por sobre otros, como es el caso del inglés en nuestros días, con la idea de una equivalencia entre ellos, es un error que empobrecerá al conjunto.
Los alfabetos en cambio, son cuantificables y es posible encontrar alfabetos óptimos, a partir de la demostración de la sección 2. La aplicación de un sistema ternario en el campo de la computación, con señales positivas, neutras y negativas, nos permitiría procesar y almacenar mejor la información.

Los temas discutidos tienen repercusiones prácticas, que no deben ser omitidas. El modelo educativo en México además de impulsar el inglés, también debería de darle un lugar importante a los idiomas de los pueblos originarios que encierran grandes riquezas. Bajo una visión errada de “lenguas inferiores”, son descuidadas, discriminadas y corren el riesgo de desaparecer.

El problema de traducción es un problema duro, sobre todo si la tarea se relega a la computación. La traducción automatizada, parte del análisis de lenguajes naturales, genera resultados aún imperfectos, a pesar de encontrarse muy desarrollada para ciertos pares de idiomas. Pero la cuestión se acentúa si considerase la falta de herramientas lingüísticas computacionales para idiomas como el wixárika. Es parte de una investigación futura la creación de un sistema capás de traducir de idiomas originarios al español y viceversa, y esto significaría la capacidad de acercar una gran cantidad de textos a los pueblos originarios en su propia lengua.

Bibliografía

Feynman, R., et al 1996 Feynman Lectures on Computation. Boston: Addison-Wesley Longman Publishing.

Fomin S. V., 1975 Sistemas de numeración. Lecciones populares de matemáticas. Moscú: Editoral MIR.

Tarski, A., 1936 “Der wahrheitsbegriff in den formalisierten sprachen,” Studia Philosophica, vol. 1, 261–405.

Brecht, B., 1997 Lieder Gedichte Chöre (1918-1933). Alemania: Suhrkamp.

Iturrio, J. L. y Gómez López, P., 1999 Gramática Wixarika I. Archivo de lenguas indígenas de México, Europa: Lincom Europa.

Gómez P., 1999 Huichol de San Andrés Cohamiata, Jalisco. Archivo de lenguas indígenas de México. México: Colegio de México.

 

---

* Barron Romero Carlos: UAM-Azcapotzalco, Prof. Tiempo Completo. Phd. Ciencias de la Computación, Universidad de Houston. Cuenta con más de 100 ponencias, 15 artículos y un cap. en libro.

** Mager Hois Jesús Manuel: Jesús Manuel Mager Hois cuenta con una licenciatura en Informática por la Universidad Nacional Autónoma de México(2015) titulado con la tesis: “El algoritmo Fringe Search como solución superior a A* en la búsqueda de caminos sobre gráficos de Malla” y actualmente se encuentra estudiando la Maestría en Ciencias de la Computación en la Universidad Autónoma Metropolitana. En su experiencia laboral sido dos veces Student Developer para Google, Inc. (2008 y 2010) en el marco del Google Summer of Code, y actualmente trabaja de Asesor Técnico en la UAM Unidad Azcapozalco. También ha participado como desarrollador proyectos de software libre como Debian y Tux4Kids. Ha impartido diversos cursos sobre Software Libre y Aprendizaje Automatizado. Su línea de investigación se centra en el Procesamiento de Lenguaje Natural con minería de datos y traducción automatizada. Es autor del artículo “acercamiento a la transformación superestructural de los Native American a través del estudio de redes sociales”.

*** Reyes Avilés Fernando: UAM-Azcapotzalco, Estudiante de la Maestría en Ciencias de la Computación con el trabajo titulado: Aplicación Android para el cálculo de filtros electrónicos activos.

1 El número es la cota superior de posibles permutaciones a partir de las 18 posiciones prefijas a la raíz verbal, y las 23 postfijas. Cada una de las posiciones puede albergar a un número de sílabas determinado o un vacío, que varía en cada posición. Para el prefijo hay 5×6×5×3×2×2×5×3×2×2×5×2×4×5×6×2×6 posibles permutaciones posibles, mientras que para el subfijo hay 2×6×10×5×2×3×2×2×2×14×3×6×8×2×3×3×2×2×3×2×2×2×2 .